Metoda Véase-Soucheho
Výchozím vztahem metody je rovnice udávající velikost kritické síly Ncr v závislosti na délce mikropiloty lp (viz literaturu [1]):
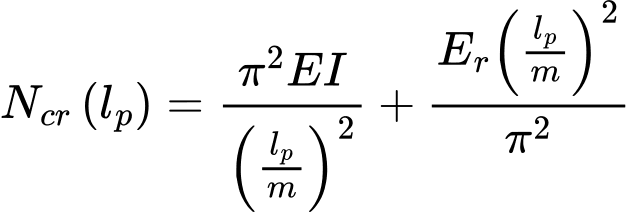
kde: | lp | - | efektivní délka mikropiloty (volná délka mikropiloty + 1/2 délky kořene) |
EI | - | ohybová tuhost dříku mikropiloty | |
Er | - | ||
m | - | počet půlvln ohybové čáry po délce mikropiloty |
Kritická síla Ncr se hledá jako minimum funkce (1). Toho je dosaženo pro délku půlvlny
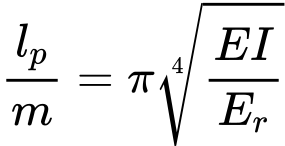
Z rovnice (2) vyplývá vztah pro počet půlvln m:
![]()
Dále se zavádí bezrozměrná veličina ω, která je dána poměrem
![]()
kde: | lv | - | délka mikropiloty nad terénem |
a další bezrozměrná veličina daná výrazem
![]()
Vztahy mezi veličinami (3), (4) a (5) jsou popsány pomocí grafů publikovaných v článku [2]. Z těchto grafů jsou pro dané hodnoty veličin ω a m stanoveny hodnoty veličiny (5) a zní je vypočtena hodnota kritické síly Ncr.
Literatura:
[1] Timoshenko, S. P.: Theory of Elastic Stability, New York, 1936
[2] Véase, Souche: Étude du fla,berment de pieux partiellernent immergés dans offrant latéralement une réaction élastique pure, Annales de I’ITBTP, No. 423, Sene Soils et Foundations, 187, mars - avril 1984, str. 38 - 60 (ve francouštině)