Polygonální smyková plocha
Řešení stability svahu při použití polygonální smykové plochy spočívá v nalezení stavu mezní rovnováhy sil, které působí na zemní těleso nad smykovou plochou. Aby bylo možno tyto síly definovat, rozdělí se zemina nad smykovou plochou na bloky dělicími rovinami. Tyto dělicí roviny jsou zpravidla voleny jako svislé, ale není to nutná podmínka, např. Sarmova metoda počítá s obecně skloněnými dělicími rovinami.
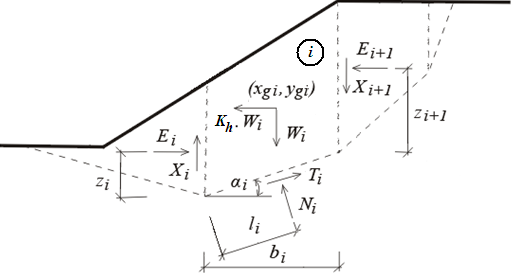 Statické schéma bloku
Statické schéma bloku
Na obrázku jsou znázorněny síly, které působí na jednotlivé bloky zeminy. Je-li oblast nad smykovou plochou rozdělena na n bloků, máme pro výpočet následujících 6n-2 neznámých: n hodnot normálových sil Ni na úsecích smykové plochy, n hodnot k nim příslušejících smykových sil Ti, n-1 hodnot normálových sil Ei mezi bloky zeminy, n-1 hodnot smykových sil Xi mezi bloky zeminy, n-1 hodnot zi, určujících působiště sil Ei, n hodnot li, určujících působiště sil Ni a jednu hodnotu stupně stability SF. Hodnoty sil Xi mohou být v některých metodách nahrazeny hodnotou sklonu sil Ei.
Pro řešení rovnováhy máme k dispozici následující soustavu rovnic: n vodorovných součtových výminek na blocích, n svislých součtových výminek na blocích, n momentových výminek na blocích a n vztahů mezi silami Ni a Ti na blocích podle Mohr-Coulombovy teorie. Celkem máme tedy 4n rovnic pro 6n-2 neznámých, z čehož plyne, že 2n-2 hodnot neznámých je nutno předem zvolit. A právě volbou těchto hodnot se liší jednotlivé použité metody řešení.
Nejčastěji bývají voleny polohy působišť jednotlivých sil nebo sklony sil mezi bloky. Řešení rovnováhy pak vede k iteračním postupům, kdy dopředu zvolené hodnoty musí jednak umožňovat splnění rovnováhy sil a jednak zajišťovat kinematickou přípustnost získaného řešení.
Program umožňuje výpočet pomocí následujících metod:
Je možné optimalizovat smykovou plochu a zjistit její nejkritičtější polohu (nejnižší stupeň stability SF).