Berechnung von Winkler-Pasternak-Konstanten aus Verformungsparametern von Böden
Die Winkler-Pasternak-Konstanten C1 und C2 werden im Programm aus der Bedingung gleicher Flexibilitätsmatrizen von unendlich steifen unendlichen Streifenfundamenten, die auf dem Winkler-Pasternak- und elastischen Untergrund ruhen, berechnet. Das Schichtmaterial wird durch die folgenden Größen charakterisiert:
Edef | - | Verformungsmodul [MPa] |
ν | - | Poissonzahl |
Eoed | ||
G | - | Schermodul [MPa] |
Davon sind Edef und ν unabhängig, die beiden anderen werden durch Beziehungen bestimmt:
![]()
und
![]()
Das Streifenfundament hat eine Breite von 2b und die Verformungszone unter dem Streifen hat eine Dicke von H.Unter der Lösung des elastischen Unterbaus versteht man die Ermittlung der Beziehung zwischen der Verschiebung und der Last des Streifenfundaments in der Form:
![]()
wobei P die Flexibilitätsmatrix ist. Durch die Berechnung einer isotropen, homogenen, elastischen Schicht unter der Fundamenttaille unter Vermeidung horizontaler Verschiebungen erhalten wir eine Flexibilitätsmatrix P der Form:
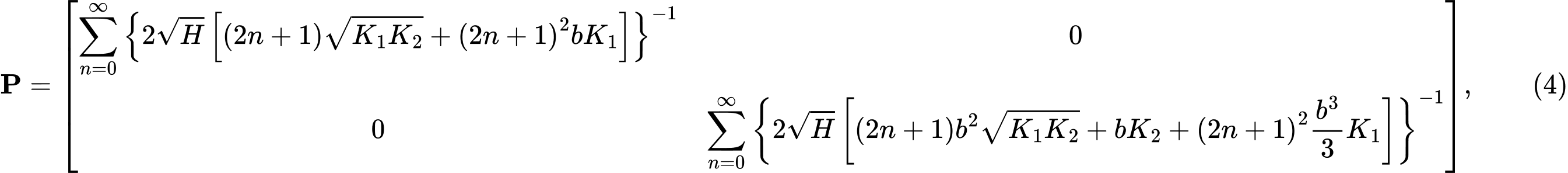
wobei
![]()
und
![]()
Durch Lösen der Differentialgleichung für das Zweiparametermodell des Untergrunds erhalten wir eine Matrix P der Form:
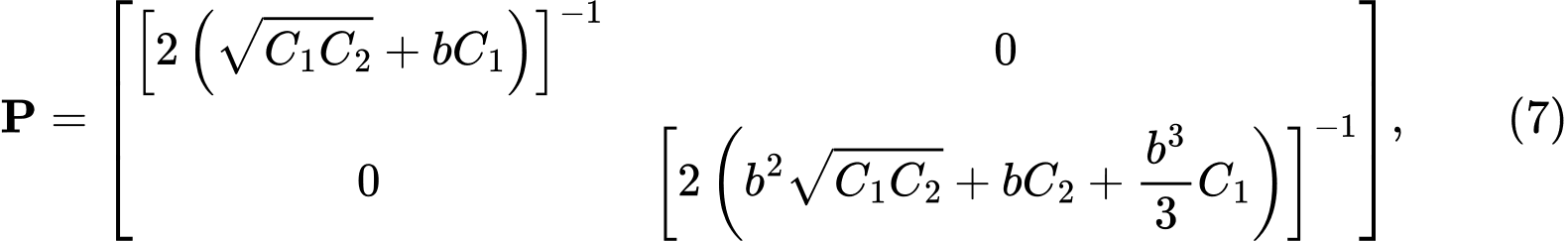
wobei C1, C2 die Konstanten des Winkler-Pasternak-Untergrundmodells sind. Ihre Werte ergeben sich aus der Bedingung, dass die Matrix P von Ausdruck (4) mit der Matrix P von Ausdruck (7) identisch sein muss. Durch Vergleich und Modifikation erhalten wir die Beziehungen:
![]()
und
![]()
wobei
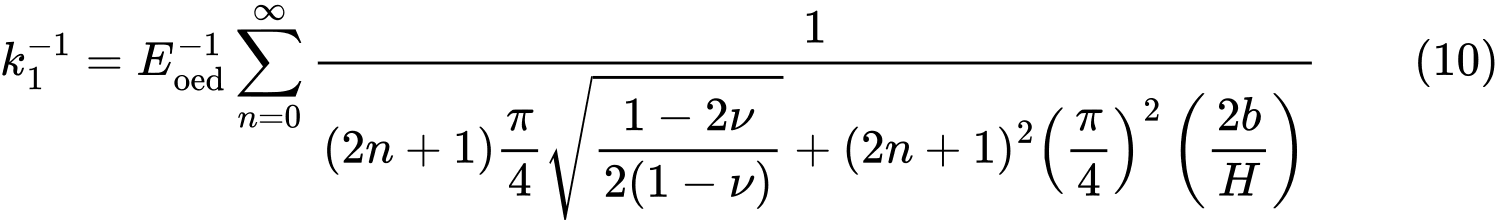
and
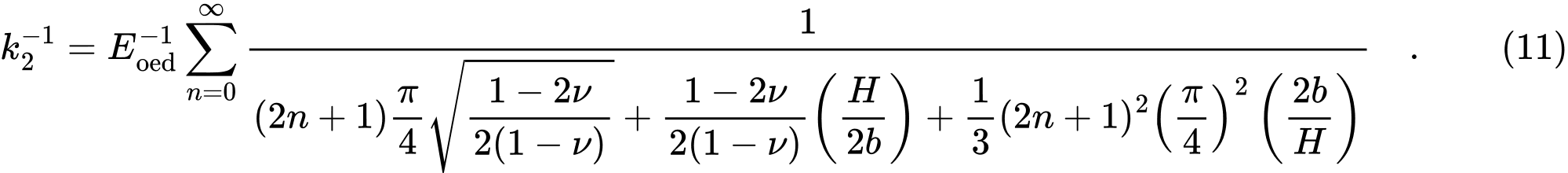
Aus den Beziehungen (8) und (9) werden die Werte von C1 und C2 direkt berechnet, während die unendlichen Summen in den Ausdrücken (10) und (11) in Geo5 für die ersten 21 Summanden durchgeführt werden.
Literatur: Kuklík, P.: Příspěvek k řešení vrstevnatého podloží, Pozemní stavby, 7-1984