Relaxamento do Solo

Online Βοήθεια

O modelo de relaxamento do solo, originalmente proposto em [1], tem aplicação na modelação de solos consideravelmente moles, com um elevado grau de compressibilidade, para os quais a aplicação do modelo de endurecimento do solo pode não ser adequado. De forma semelhante ao modelo de endurecimento do solo, o modelo de relaxamento do solo é apresentado por duas superfícies de cedência. A superfície de cedência de cisalhamento baseia-se no critério de cedência de Matsuoka-Nakai e a prensa de compressão é formulada com base no modelo de Cam-clay Generalizado. As suas projeções no plano de desvio correspondem a curvas convexas suavizadas que intersetam os vértices do modelo de Mohr-Coulomb. A figura seguinte mostra uma representação gráfica.

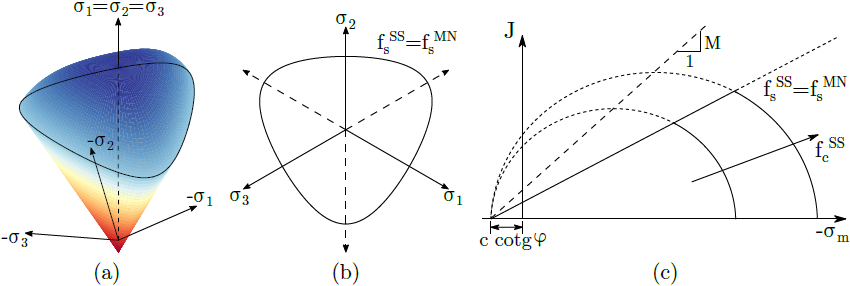a) superfície de cedência no espaço de tensão principal, b) projeção no plano de desvio e principal e c) no plano meridiano

Contrariamente ao modelo de Cam-clay generalizado, a inclinação da linha de estado crítico M é definida em relação ao coeficiente de empuxo de terra lateral em repouso para solos normalmente consolidados K₀^N e aos parâmetros de rigidez κ^*, λ^* de acordo com

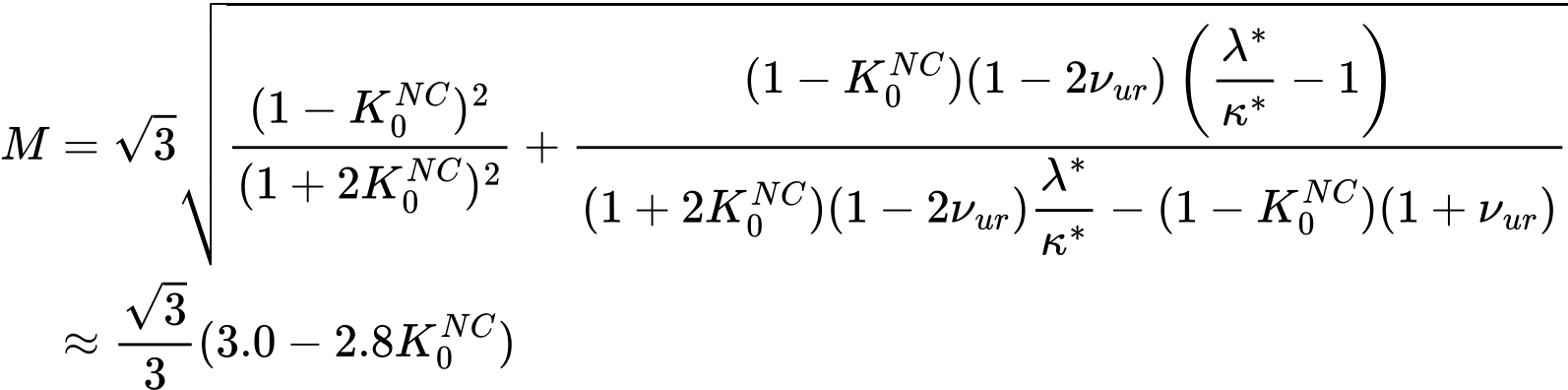
Pode encontrar mais detalhes acerca dos parâmetros κ^*, λ^* na descrição do modelo de Cam-clay modificado. A razão para esta definição está relacionada com o facto de o valor do parâmetro M, que no modelo de Cam-clay modificado permite uma resistência ao cisalhamento correta, pode indicar que o valor de K₀^NC excede consideravelmente o valor recomendado pela fórmula de Jaky para um dado valor do ângulo de atrito interno φ. Pode encontrar mais detalhes em [1].

Assume-se que a superfície de cedência de cisalhamento está em concordância com o comportamento descrito pelo modelo material elástico-perfeitamente plástico. Por outro lado, a prensa de compressão, apenas permite endurecimento, contrariamente do modelo de Cam-clay generalizado. Por outras palavras, a pressão de pré-consolidação p_c motiva a que a evolução da compressão tenha tendência sempre positiva. Veja, também, a descrição do modelo de Cam-clay modificado. Esta limitação implica algumas restrições na seleção dos parâmetros do modelo, particularmente no valores do ângulo de atrito interno φ. Tal implica a satisfação da seguinte condição

Esta condição deve ser satisfeita ainda que

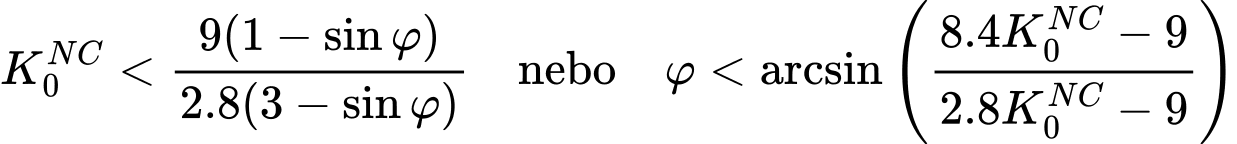
A figura seguinte mostra uma representação gráfica da relação entre a superfície de cedência de cisalhamento e a prensa de compressão, para dois valores diferentes de K₀^NC e para vários valores do ângulo de atrito interno φ, considerando valores fixos para os parâmetros κ^*, λ^*, ν. É evidente que para a combinação de M(K₀^NC = 0.6) = 0.774 e φ = 40°, as condições acimam não são satisfeitas, sendo que se obtém φ_max = 33.2° < φ = 40° para a primeira condição, enquanto que para a segunda condição se obtém φ_max = 32.8°, de acordo com a linha verde da figura (b).

Uma vez que as projeções de ambas as superfícies de cedência no plano meridiano dependem do ângulo de Lode, estas figuras correspondem ao caso de compressão triaxial. Pode encontrar detalhes acerca da estimativa de relaxamento através do modelo de Cam-clay generalizado na descrição deste modelo, ou também pode ver a comparação de estimativas entre os modelos de Cam-clay modificado e de Cam-clay generalizado aqui. Pode encontrar mais detalhes no manual teórico.

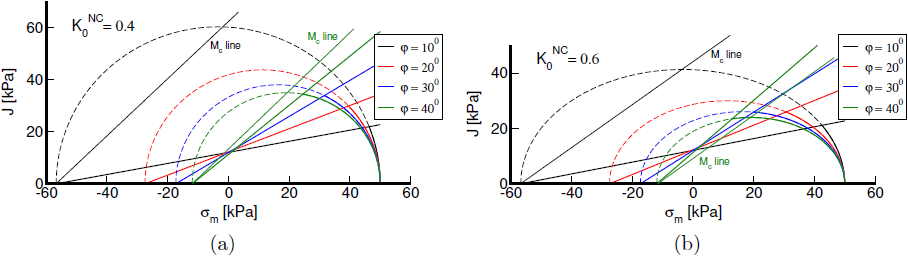Compressão e superfícies de cedência de cisalhamento: : φ e K₀^NC: a) K₀^NC =0.4, b) K₀^NC =0.6

A evolução da pressão de pré-consolidação p_c, assim como o significado dos parâmetros que definem as relações básicas da prensa de compressão estão detalhadas na descrição do modelo de Cam-clay modificado. A função do potencial plástico que conduz ao desenvolvimento de deformações plásticas na região controlada pela superfície de cedência de cisalhamento é idêntica à adotada para o modelo de Drucker-Prager. Assim sendo, é independente ao ângulo de Lode. Por outro lado, depende do ângulo de dilatação ψ (M_ψ = M_ψ(ψ)). Normalmente, assume-se que φ ≠ ψ, o que corresponde à regra de fluxo não associado. De forma idêntica ao modelo de Drucker-Prager, o valor da dilatação (desenvolvimento de deformações plásticas volumétricas durante o cisalhamento plástico) pode ser limitado pela introdução do índice de vazios máximo e_max, para o qual é expectável atingir o estado crítico em que ψ = 0.

A tabela seguinte apresenta os parâmetros que definem o modelo de relaxamento do solo.

Símbolo	Unidade	Descrição
		Inclinação da linha de dilatação
		Inclinação da linha de consolidação normal
		Índice de vazios máximo no diagrama
		Coeficiente de Poisson
	[kPa]	Coeficiente de coesão efetiva
		Ângulo de atrito interno efetivo
		Ângulo de dilatação
		Coeficiente de empuxo de terra lateral em repouso para solos normalmente consolidados
		Índice de vazios máximo para terminar a dilatação (ao limitar a dilatação)
		Rácio de sobre-consolidação
	[kPa]	Pressão de pré-consolidação
	[1/K]	Coeficiente de dilatação térmica (ao considerar efeitos de temperatura)
		Ângulo de atrito em estado crítico (não inserido)
	[kPa]	Pressão de pré-consolidação (não inserida)

De forma semelhante ao modelo de Cam-clay modificado, o módulo de Young não é introduzido diretamente, mas sim determinado a partir do módulo de dilatação K_s dado por

A evolução da rigidez depende do valor atual da tensão média efetiva σ_m, tal como para o modelo de Cam-clay modificado. A definição dos valores iniciais da tensão de pré-consolidação p_cⁱⁿ, do módulo de dilatação K_sⁱⁿ e do índice de vazios inicial está detalhado na descrição do modelo de Cam-clay modificado.

Tal está relacionado com a seleção da etapa inicial de carregamento, que implica valores muito reduzidos para que a tensão inicial seja suficientemente reduzida. De forma a acelerar a convergência, é adequado explorar o número mínimo de iterações para uma única etapa de carregamento. A influência da magnitude da etapa inicial de carregamento na evolução da tensão e da deformação está descrita em detalhe aqui.

Contrariamente aos restantes modelos do tipo de Mohr-Coulomb, o índice de vazios inicial e_in, que corresponde ao estado do solo no final da primeira etapa de cálculo (tensão geostática), não é introduzido mas sim determinado computacionalmente a partir do valor definido para o índice de vazios e₀ e para o estado de tensão atual, conforme descrito para o modelo de Cam-clay modificado.

O modelo permite ajustar o valor inicial da pressão de pré-consolidação p_c em função do grau de pré-consolidação esperado, através dos parâmetros e . Pode encontrar mais detalhes aqui. De notar que esta opção apenas está disponível ao definir a tensão geostática inicial com recurso ao procedimento K₀.

No caso de a análise implicar condições não drenadas, é possível recorrer apenas ao Tipo (1): análise para tensão efetiva (c_ef, φ_e).

O modelo de relaxamento do solo também permite realizar análises de estabilidade. No entanto, esta opção apenas está disponível ao executar a análise de estabilidade dentro da etapa de construção respetiva. Neste caso, a prensa de compressão é desativada. Assim, apenas fica ativa a superfície de cedência de cisalhamento. O problema é resolvido de forma gradual, reduzindo os parâmetros de resistência ao cisalhamento de pico c, φ de forma idêntica ao descrito para o modelo de Drucker-Prager.

A performance do modelo em ensaios laboratoriais é examinada aqui, incluindo a comparação com o modelo de Cam-clay modificado e a influência da magnitude da etapa inicial de carregamento.

A implementação do modelo material de relaxamento do solo no programa GEO5 MEF está descrito em detalhe no manual teórico.

Bibliografia:

[1] R.B.J. Brinkgreve, Geomaterial Models and Numerical Analysis of Softening, PhD thesis, Technische Universiteit Delft, 1994. Available at https://repository.tudelft.nl/record/uuid:6738de62-4dde-45b0-b3bd-3635504767c2.