Verification according to AISC 360-22 (LRFD, ASD)
Check of shear
Shear stress resistance for composite cross section with concreted steel cross section is determined conservatively as shear capacity of steel profile.
Nominal shear strength for round cross section filled with concrete is provided by:
![]()
where: | Av | - | shear area of steel profile when for a round section is equal to 2As / π |
Fy | - | specified minimum yield stress | |
Kc | - | conservatively considered as 1.0 | |
Ac | - | area of concrete | |
fc' | - | specified compressive strength of concrete |
Check for shear force is determined as:
- for LRFD: Q / (Vn ϕv ) ≤ 1.0
- for ASD: Q / (Vn / Ωv ) ≤ 1.0
Check for compressive
Nominal compressive strength for concreted steel cross section is provided by:
![]()
Nominal compressive strength of "non-compact" round HSS filled with concrete is provided by:
where: | As | - | area of structural steel section |
Ac | - | area of concrete |
Nominal compressive strength of "compact" round HSS filled with concrete is provided by:
![]()
![]()
![]()
where: | λp, λr | - | are width-to-thickness ratios due to AISC 360 and Tab.I1.1a |
λ | - | width-to-thickness ratio = D / t | |
D | - | outside diameter of round HSS | |
t | - | thickness of round HSS |
Nominal compressive strength of "slender" round HSS filled with concrete is provided by:
![]()
where: | Fn | - | critical buckling stress |
![]()
where: | Es | - | modulus of elasticity of steel |
Available compressive strength is determined as:
- for LRFD: Pc = Pn ϕc
- for ASD: Pc = Pn / Ωc
Check for flexure
Nominal flexural strength is determined from the interaction diagram for corresponding distribution of normal stress calculated with influence of bending moment.
For composite cross sections with concreted steel cross section the following normal stress distribution is assumed:
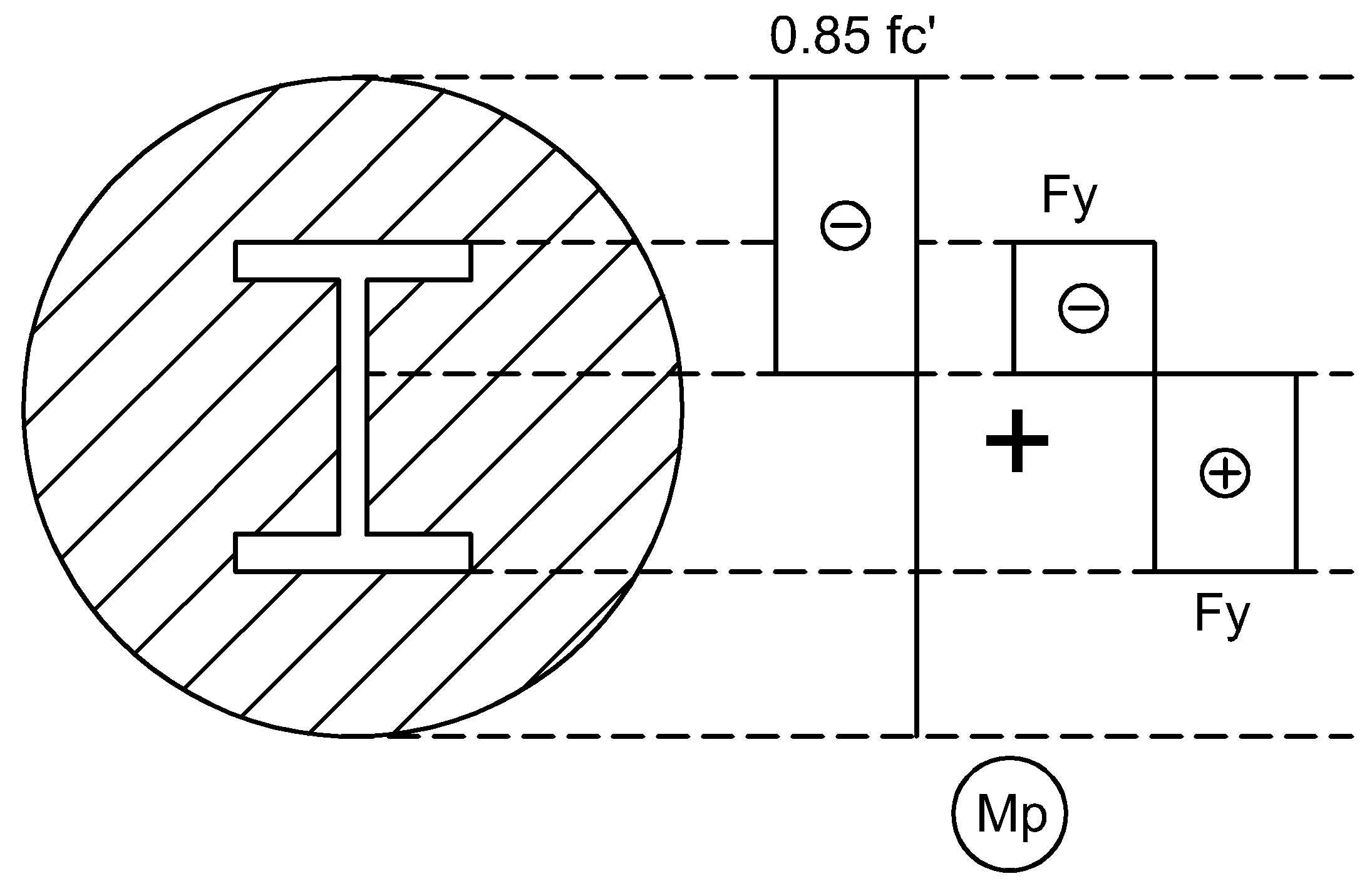
Nominal flexural strength is provided as:
![]()
where: | Mp | - | moment corresponding to plastic stress distribution over the composite cross section |
For round HSS cross sections filled with concrete the following normal stress distribution depending on D/t ratio is assumed:
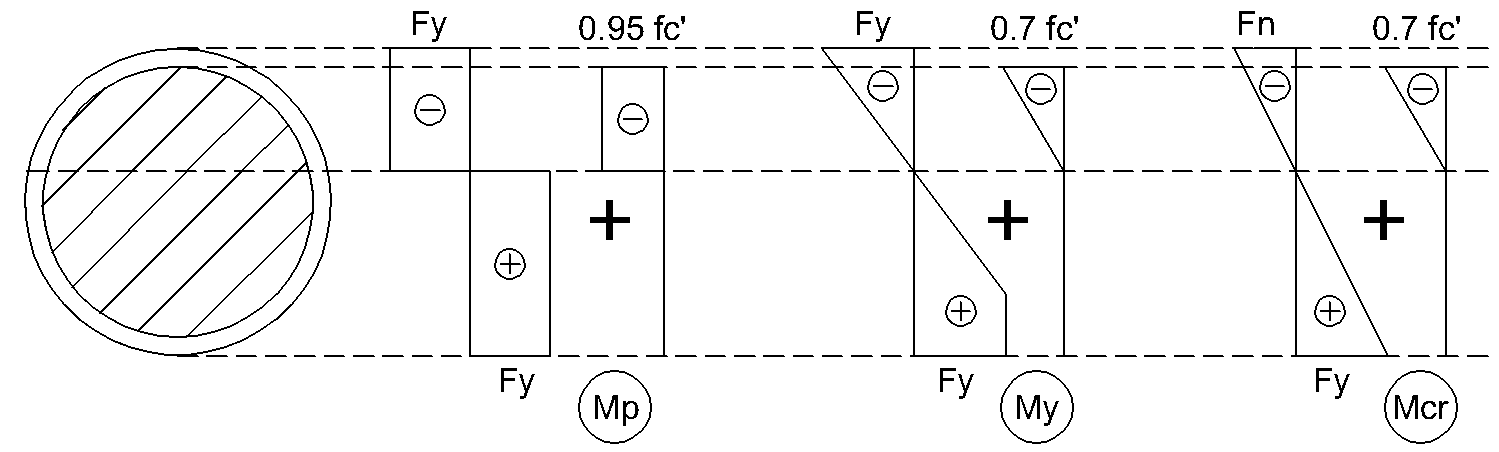
Nominal flexural strength of "compact" round HSS filled with concrete is provided by:
![]()
Nominal flexural strength of "non-compact" round HSS filled with concrete is provided by:
![]()
where: | My | - | yield moment corresponding to elastic-plastic stress distribution over the cross section |
λp, λr | - | width-to-thickness ratios determined from Table I1.1b |
Nominal flexural strength of slender" round HSS filled with concrete is provided by:
![]()
where: | Mcr | - | first yield moment corresponding to elastic stress distribution over the cross section |
Available flexural strength is determined as:
- for LRFD: Mcx = Mn ϕb
- for ASD: Mcx = Mn / Ωb
Check for axial force and flexure
Check for axial force and flexure is provided by formula:
- if: N / Pc ≥ 0.2
![]()
- if: N / Pc < 0.2
![]()