Nichtlineare Modelle
Introducing nonlinear material models allows for a considerable improvement in capturing a real response of soils to the applied load. In the GEO5 FEM program these programs are formulated either on the basis of theory of plasticity or hypoplasticity. Application of these models is typically accompanied by the evolution of plastic strains. These strains can be exploited to graphically indicate potential failure zones, e.g., in the form of the localized equivalent deviatoric plastic strain. The theory of hypoplasticity does not provide such an option. Graphical representation of expected failure regions can be in this particular case provided by plotting the parameter mobilized shear strength.
Evolution of plastic strains is driven by the yield surface representing in the stress space the boundary between an elastic and plastic material behavior. Mathematical formulation of the yield surface then represents a certain failure condition (yield function). In a general stress state the yield surface is typically formulated with the help of invariant stress and strain measures. This function remains either constant for the entire loading range (elastic-perfectly plastic material models) or may evolve in dependence on the current state of stress and plastic strain (elasto-plastic material models with hardening/softening or Critical state models). At equilibrium, the material point is always found either inside the yield surface (elastic response) or on its boundary (plastic response). Further details can be found in the theoretical manual.
As an illustrative example we consider a graphical representation of the Mises yield surface in the principal stress space. A common way of visualization includes projections of the yield surface into a deviatoric and a meridian plane, σm is the mean stress, J is the equivalent deviatoric measure of deviatoric stress components, and θ is the Lode angle. The deviatoric plane is perpendicular to the hydrostatic axis where σ1 = σ2 = σ3 = σm.
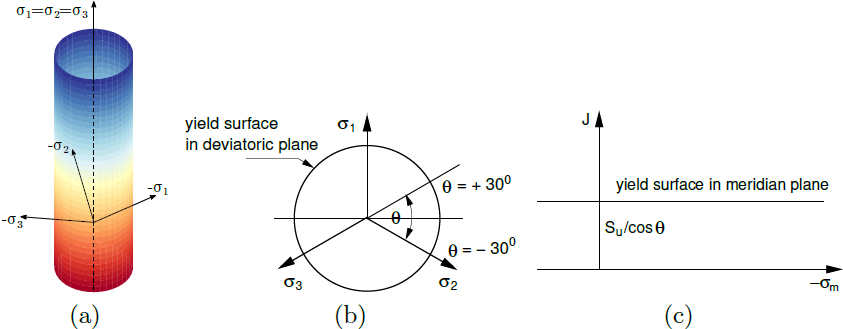 a) yield surface in principal stress space, b) projection into deviatoric and c) meridian planes
a) yield surface in principal stress space, b) projection into deviatoric and c) meridian planes
- Elastic-perfectly plastic material models. The Drucker-Prager, Mohr-Coulomb, and Hoek-Brown models fall into this group of material models.
- Elastic-plastic material models with hardening/softening. The Hardening soil, Soft soil, and Modified Mohr-Coulomb models fall into this group of material models.
- Critical state models. The Modified Cam-clay, Generalized Cam-clay, and Hypoplastic clay models fall into this group of material models.
Note: Unlike the GEO5 FEM program, the mathematical expressions and graphical representation of constitutive relationships and yield and potential surfaces assume, similarly to the theoretical manual, standard elasticity sign convention, i.e., tensile stress is positive and compressive stress is negative (σ > 0 - tension, σ < 0 - compression).